“Tanteando en la mampostería que bordeaba el
pozo logré desprender un fragmento menudo y lo tiré al abismo. Durante largos
segundos escuché cómo repercutía al golpear en su descenso las paredes del
pozo; hubo, por fin, un chapoteo en el agua, al cual sucedieron sonoros ecos.”
El
fragmento anterior corresponde a uno de los relatos breves más célebres de
Edgar Allan Poe: El pozo y el péndulo (The pit and the pendulum) publicado
en 1842. En él se narra la aterradora experiencia de un hombre anónimo sentenciado
a muerte durante la oscura época de la Inquisición española.
A lo
largo de las breves pero intensas páginas que conforman el relato se describen
las dramáticas sensaciones por las que pasa el protagonista, condenado a una
terrible tortura. Encerrado en lo más profundo y oscuro de una cripta, una
cuerda pende fija del techo oscilando de un lado a otro, como si se tratase del
péndulo de un antiguo reloj de pared, en cuyo extremo móvil se encuentra una enorme
hoja afilada en forma de media luna.
“Yacía ahora de espaldas, completamente
estirado, sobre una especie de bastidor de madera.”
 De
esta guisa, atado firmemente, excepto por uno de sus brazos, que le permite
acceder con cierta dificultad al plato de comida, el hombre va observando con
horror cómo el péndulo va descendiendo paulatinamente hasta que por fin selle
su terrorífico destino para siempre.
De
esta guisa, atado firmemente, excepto por uno de sus brazos, que le permite
acceder con cierta dificultad al plato de comida, el hombre va observando con
horror cómo el péndulo va descendiendo paulatinamente hasta que por fin selle
su terrorífico destino para siempre.
“Mirando hacia arriba observé el techo de mi
prisión. Tendría unos treinta o cuarenta pies de alto, y su construcción se
asemejaba a la de los muros.”
Bien,
como esto de los pies es una unidad de longitud un tanto anglosajona,
consideraré que la mazmorra tenía una altura de algo más de 10 metros (10
metros exactamente desde el techo hasta el tórax del prisionero y unas cuantas
decenas de centímetros más desde éste hasta el suelo, contando con el espesor
de su cuerpo y la altura del bastidor de madera sobre el que se encontraba
tumbado).
En
cuanto al tamaño del cubículo, también disponemos de una vaga descripción por
parte del protagonista. En uno de los párrafos afirma lo siguiente:
“Mucho me había equivocado sobre su tamaño.
El circuito completo de los muros no pasaba de unas veinticinco yardas [...]
Mi prisión tenía forma cuadrada.”
¡Vaya!
Ya estamos otra vez con las puñeteras unidades que no son del Sistema Internacional.
En fin, admitiré que el lado del cuadrado era de 5 metros de longitud, es
decir, la cuchilla podía oscilar horizontalmente a cada lado no más de 2,5
metros desde su posición natural de equilibrio, la vertical.
Al
principio, el hombre observa el péndulo en las alturas, relativamente lejos de
su alcance, pero...
“Habría pasado una media hora, quizá una hora
entera […] antes de volver a fijar los ojos en lo alto. […] La carrera del
péndulo había aumentado, aproximadamente, en una yarda. Como consecuencia
natural, su velocidad era mucho mayor. Pero lo que me perturbó fue la idea de
que el péndulo había descendido perceptiblemente.”
Ahora
es cuando os tengo que recordar que desempolvéis vuestros olvidados
conocimientos de física, en concreto, el requete-archi-repetido péndulo simple.
¿Os viene a la memoria? Bueno, pues lo más relevante de este dispositivo,
formado por una cuerda en cuyo extremo oscilante se coloca un pequeño objeto
sin masa denominado, comúnmente, lenteja, es que su período no depende en absoluto
de la amplitud angular, sino únicamente de la longitud de la cuerda. ¿Qué
significa esto? Pues que si utilizáis siempre el mismo péndulo pero lo dejáis
oscilar soltándolo desde posiciones distintas (más cerca o más lejos de la
posición vertical, como os apetezca) comprobaréis que el tiempo que tarda en
recorrer una oscilación completa, de un extremo al otro y vuelta de nuevo a la
posición inicial, es siempre el mismo (a este lapso de tiempo se le denomina
período del péndulo, y el ángulo que forma la cuerda con la vertical recibe el
nombre de amplitud angular). Solamente conseguiréis que el período aumente si
incrementáis la longitud de la cuerda (análogamente, que disminuya el período
acortando la longitud de la misma).
Según
esto, la pregunta que surge es la siguiente: ¿se comporta el péndulo del relato
de Edgar A. Poe como un péndulo simple? Obviamente, la respuesta es no, como
vosotros mismos podéis deducir de lo dicho por el reo dos párrafos más arriba.
No hay manera de que descendiendo el péndulo perceptiblemente, es decir, de que aumentando su longitud, la
carrera de aquél aumente a su vez. Así pues, ¿cómo solucionar esta cuestión?
Veamos,
la forma más fácil que se me ocurre de salir del aprieto en que os he puesto es
decir la verdad y la verdad no es otra que ésta: vuestros profesores os
engañaron. Los péndulos simples no existen. En realidad, lo que vuestros
profesores os explicaron en su día es que un péndulo se comporta,
aproximadamente, como simple cuando la amplitud angular es pequeña, esto es,
cuando lo dejáis oscilar soltándolo desde una posición muy cerquita de la
vertical. En este caso, la ecuación matemática que rige su comportamiento se
puede simplificar notablemente y su resolución es extremadamente sencilla, y es
la que casi todos conocéis. Sin embargo, la ecuación rigurosa, la verdadera, para entendernos, resulta algo más compleja, al igual que su solución.
Bien,
intentemos solucionar la ecuación rigurosa, la buena, la que describe las
oscilaciones de un péndulo que no se comporta como simple. En la literatura
científica se pueden hallar expresiones analíticas exactas para la solución de
la ecuación anterior, pero involucran a las denominadas funciones de Bessel y
no me detendré ahora en ellas. En cambio, sí que resulta mucho más interesante
resolver el problema de forma numérica, es decir, acudiendo a las simulaciones
mediante el empleo de un ordenador y un software adecuado.
 |
| Figura 1 |
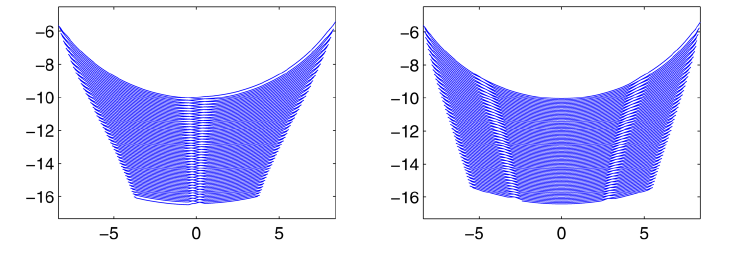
Cuando
se procede de esta manera, es necesario hacer ciertas suposiciones que sean
razonables. Una de estas suposiciones consiste en admitir que la velocidad a la
que aumenta la longitud del péndulo es constante. Al hacer esto, se comprueba
inmediatamente que aunque la distancia horizontal que recorre la cuchilla que
pende del extremo de la cuerda va aumentando lentamente (Figura 1: el eje de abscisas representa la distancia horizontal recorrida por la cuchilla, mientras que el eje de ordenadas da cuenta de la longitud de la cuerda. Mirad la gráfica de arriba abajo y veréis las oscilaciones del péndulo a medida que desciende y cómo la distancia horizontal alcanzada por la hoja asesina aumenta lentamente), no sucede lo mismo con
la amplitud angular, la cual disminuye ostensiblemente a medida que va
transcurriendo el tiempo (Figura 2: el eje de abscisas representa el tiempo en segundos y el eje de ordenadas el ángulo descrito por el péndulo respecto a la vertical. Se ve fácilmente la rápida disminución de la amplitud angular con el tiempo, es decir, a medida que el péndulo va descendiendo hacia el condenado). Por poner unos números que ilustren lo dicho, imaginemos
que la longitud de la cuerda crece a un ritmo constante de 10 centímetros
cada segundo. Si el péndulo que amenaza la vida del prisionero tuviese una
longitud inicial de 10 metros (y daos cuenta de que esta longitud es ya la más
pesimista, la que despedazaría a nuestro protagonista, según afirmamos más
arriba, en base a sus propias estimaciones visuales) y lo soltásemos desde una
posición que formase un ángulo justo por encima de unos 57º (1 radián) con la
vertical, al cabo de tan sólo dos minutos, la amplitud angular habría descendido hasta
la mitad, unos 28º. Mientras tanto, la distancia a la que habría descendido la
cuchilla se habría incrementado hasta los 22 metros.
 |
| Figura 2 |
Una
vez llegados a este punto, parece que el relato de Poe no se ajusta
excesivamente a los resultados que nos proporcionan las simulaciones mediante
ordenador. Así como en unas partes del texto el condenado admite que el péndulo
ha descendido perceptiblemente en una media hora, quizá una hora, más
adelante podemos leer lo siguiente:
“Pulgada a pulgada, con un descenso que sólo
podía apreciarse después de intervalos que parecían siglos…, más y más íbase
aproximando. Pasaron días, puede ser que muchos días, antes de que oscilara tan
cerca de mí que parecía abanicarme con su acre aliento. [...] Ya pasaba
vibrando a tres pulgadas de mi pecho.”
 El
párrafo anterior parece contradecir el "perceptible" descenso del
péndulo en otro momento de la narración en tan sólo unos cuantos minutos. De
hecho, admitiendo el caso más benévolo en el párrafo previo, o sea, que
hubiesen transcurrido únicamente dos días, la velocidad de descenso de la
cuchilla rondaría los 19 centímetros por hora. ¿A qué se debe esta
discordancia? ¿Constituye una mera licencia literaria del autor? ¿Es el
resultado de la, comprensiblemente, perturbada mente y errónea percepción del
tiempo por parte del prisionero, a punto de encontrarse cara a cara con la
muerte? ¿O puede explicarse físicamente, de alguna manera?
El
párrafo anterior parece contradecir el "perceptible" descenso del
péndulo en otro momento de la narración en tan sólo unos cuantos minutos. De
hecho, admitiendo el caso más benévolo en el párrafo previo, o sea, que
hubiesen transcurrido únicamente dos días, la velocidad de descenso de la
cuchilla rondaría los 19 centímetros por hora. ¿A qué se debe esta
discordancia? ¿Constituye una mera licencia literaria del autor? ¿Es el
resultado de la, comprensiblemente, perturbada mente y errónea percepción del
tiempo por parte del prisionero, a punto de encontrarse cara a cara con la
muerte? ¿O puede explicarse físicamente, de alguna manera?
Me
centraré en este último interrogante, como no puede ser de otra forma en un
blog dedicado a la física. ¿Qué esperabais? Para soluciones relacionadas con la
psicología podéis acudir a sitios menos divertidos y más apropiados.
Me
vais a permitir que os sugiera una solución un tanto retorcida y algo
sofisticada para que el comportamiento del péndulo del relato se aproxime a la
realidad del relato de Poe. Para ello, os vuelvo a pedir que hagáis un poco de memoria y
retrocedáis por un momento a vuestra infancia. Cerrad los ojos e imaginaos que
estáis subidos en un columpio del parque. Comenzáis a impulsaros y queréis ir
cada vez más arriba en vuestro alucinante viajecito. ¿Qué hacíais? ¿No
estirabais las piernas cuando llegabais al punto más alto y después las
encogíais, las plegabais al pasar por la vertical? ¿Y no veis una semejanza
manifiesta entre un columpio y el péndulo mortal y la cuchilla del relato que
nos ocupa? Pues eso...
 |
| Figura 3 |
 |
| Figura 4 |
“Vi que después de diez o doce oscilaciones
el acero se pondría en contacto con mi ropa.”
Con esta entrada participo en la XLVIII Edición del Carnaval de la
Física, alojado esta vez en el blog de Daniel Martín Reina (@monzonete) La Aventura de la Ciencia.
Fuente original:
Matthew McMillan, David Blasing, and Heather M. Whitney Radial forcing and Edgar Allan Poe's lengthening pendulum, American Journal of Physics, Vol. 81 (9), September 2013

En el encabezado del post he marcado el ítem "Obra maestra". Porque lo es. Punto.
ResponderEliminarGracias, Sergio.
Muchas gracias, Dani, por tomarte el tiempo para leerlo.
EliminarYa lo ha dicho Dani, ayer bromeé con el tema del ángulo pero no me imaginaba que todo acabara con cálculo numérico incluido ^_^
ResponderEliminarBuf, y a veces incluso aparece caos. Los péndulos son megapuñeteros y trajeron de cabeza a los mismísimos Galileo y Newton. Un tema que da mucho mucho juego.
EliminarEstoy con Dani, es una "OBRA MAESTRA". Una verdadera lección de cómo lograr que la gente se apasione por la física y aprenda.
ResponderEliminarEn tus libros y entradas recupero lo que sentía la Laurita cuando descubrió la Física a los 12 años y tuvo clarísimo que quería dedicarse a ello porque no había nada más fascinante. Cuando le daba pena el día que no había clase porque estaba esperando lo siguiente que iban a explicar… He tenido profesores buenos, normalillos y nefastos, pero personas que me transmitan esa pasión por la física sólo dos, mi primer profesor y amigo Sebastià y tú.
Gracias por todos estos miércoles, por continuar aquí.
Un beso muy fuerte
P.D. Ni te imaginas la ilusión que me hace verme en ese Blogroll, :____________)
¿Hay un emoticono para la cara ruborizada?
EliminarPersonalmente yo interpretaba que los inquisidores regulaban el mecanismo en función del estado del preso para maximizar su angustia.
ResponderEliminarUn pequeño apunte: en una habitación de planta cuadrada de 5m de lado, es posible que un péndulo que cuelga del centro del techo oscile más de 2,5m a cada lado respecto a la vertical, si lo hace paralelamente a una diagonal de la planta.
Buenísimo, te has ganado mi follow :D y es lo primero que leo de tu sitio, muy interesante e inspirador!
ResponderEliminar